Any professionally taught programmer eventually has to learn binary trees. Some high school students are exposed early as part of the AP Computer Science AB exam but most have to learn it as part of a data structures course in college.
There are three ways to read a binary tree:
- Prefix: Root node, then left child, then right child
- Infix: Left child, then root node, then right child
- Postfix: Left child, then right child, then root node
Take, for example, this really simple binary tree:
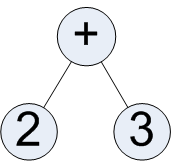
The ways to read this are:
- Prefix: + 2 3
- Infix: 2 + 3
- Postfix: 2 3 +
The infix reading of this tree resembles (and, in fact, is) the standard way we write and interpret simple mathematical equations. "Two plus three equals..." (As an aside, all simple mathematical equations can be expressed as a binary tree. I'm not happy with the tools I have available to render trees right now so I will leave this as an exercise for you, the reader.)
The postfix reading should be familiar to anyone who owns a Hewlett-Packard graphing calculator. This form of representing mathematical equations is most commonly referred to as Reverse Polish notation. Postfix ordering of mathematical expressions is commonly used for rendering stack-based calculators, usually in assignments for a programming class.
The prefix reading resembles the standard way we use constructs in programming languages. If we had to represent "2 + 3" using a function, we would write something like plus( 2, 3 ). This is most clearly shown with LISP's construct ( + 2 3 ). Haskell's backtick operators around infix operators, e.g. `div`, have a side effect of reminding programmers that most functions are prefix-oriented.
So why discuss reading binary trees anyway? In a classroom, teaching the student how to read a binary tree leads to the student being able to program a way to read a binary tree which will then lead to other things. Here, I discuss reading them as background for the next post which may itself lead to other things.
Edit: (11 May 2009) Unfortunately, in the process of writing the next post, I realized that the entire premise of the post was invalid. So the next post will probably not have anything to do with trees.